http://acmicpc.info/archives/1703
http://www.cnblogs.com/kuangbin/p/3744817.html
Problem A. Matrix
Analysis:
【贪心】【递归】【生成链】
比较容易写错。
。。。不难归纳生成矩阵的性质。
1. 每行的数单调递增。(。。。因为每个格子的数只有可能减小,且最大的数一定出现在行末尾)
2. 每行的 size 单调递减。。。(因为下方的数,总是被后出现的较小的数顶下去的。。)
观察一些数据。。。
4 3 2 1 3 1 2 1 4
。。这个显然是 4 2 1 3 。。。。
。。。考虑定位当前最大的数在 输入序列 中的位置。。
。。为了得到逆序字典序最大。。我们希望它可以尽可能的往后。。
。。。我们从 4 开始。。向上剥开生成 4 的链 1-2-4 。。。但是发现此时 1 并不是其所在行的最末尾数。。。
。。因此 3 必须在这条链之后插入。。。。于是我们优先递归 3 。。。
于是就是两个函数。。。
bool gao(); 从大到小枚举没有定位的数,将它们一次 bao() 开。。。
bool bao(int ii); 递归尝试剥开 ii 。。C[ii] 表示 ii 所在的行号,-1 表示已经定位。。。
这样不需要二分。。。总的复杂度是 O(n) 、。。。
Problem B. Beautiful Garden
Brief description:
。。。给定一组序列,修改最少的元素,使得该序列排序后是一个等差序列。
Analysis:
观察一些数据。。 1 4 6 100 1000 10000 结果是。。 1 *2 *3 4 *5 6
。。。最终序列的首位置一定可以是原序列中的某个数(因为修改的任意性,你可以尽可能的放到后面。)
。。除此之外,还可以至少有一个数不修改。。。枚举这两个数。。。
。。。再枚举公差 dd。。
(。。。注意这一步不需要枚举所有可能的公差。。
。我们只需要枚举这两个数之间包含的数的个数。。
..。而这个值不会超过 n-2 。。)
注意:
。。long long ?(这种题目数据是 int 但是运算过程中有可能是 long long 的要尤为小心。。
。dd = 0 ?
n <= 2?
Problem C. Champions League
Brief description:
。。。。这个题真是相当之赞。。。
。。不妨先来看一种 naive 的做法。。。。
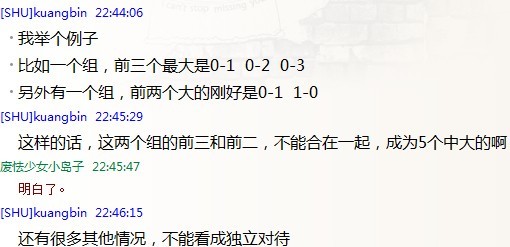
。。。对每一个 group。。。枚举 2^3 种情况。(考虑 0-1, 0-2, 0-3 、、。。)。。。
。。每次,得到 6 对数,对每对数取 max 得到这一天的最大得分。。。
。。排序后取前缀和。。就可以得到容量 1~6、6 个 物品。。。然后外围 0/1 背包。。。
。。不幸的是。。这个做法是只能保证 group 内没有冲突的。。。
。。。。这样一来我们似乎需要加维来描述这种结对信息。。。。。但是稍作尝试后我们发现这样处理讨论起来会过于复杂。。。
。。不如直接暴力 1<<6 状态压缩 DP 来的有效。。。。
。。。但是这样会 TLE。。我们发现其实只需要保留最大的 6 个小组即可。
。。 (把多有 a[][] 塞到一个 vector 里从大到小排序比较。。)。。。
。。(因为我们只会取 6 天。。最差情况。如果每个 group 只转播一场。。也只需要用到前 6 个小组。。)
。。。。




 Alca
Alca Amber
Amber Belleve Invis
Belleve Invis Chensiting123
Chensiting123 Edward_mj
Edward_mj Fotile96
Fotile96 Hlworld
Hlworld Kuangbin
Kuangbin Liyaos
Liyaos Lwins
Lwins LYPenny
LYPenny Mato 完整版
Mato 完整版 Mikeni2006
Mikeni2006 Mzry
Mzry Nagatsuki
Nagatsuki Neko13
Neko13 Oneplus
Oneplus Rukata
Rukata Seter
Seter Sevenkplus
Sevenkplus Sevenzero
Sevenzero Shirleycrow
Shirleycrow Vfleaking
Vfleaking wangzhpp
wangzhpp Watashi
Watashi WJMZBMR
WJMZBMR Wywcgs
Wywcgs XadillaX
XadillaX Yangzhe
Yangzhe 三途川玉子
三途川玉子 About.me
About.me Vijos
Vijos
