http://www.codechef.com/JAN13/
Level 2. Dividing Products
Brief description:
定义 “交错乘除” DIVPRO(x) 为。。 x 的十进制展开后。。交错相乘相除。。
。。例如 x = 1234 那么 DIVPRO(x) = 1 / 2 * 3 / 4 = 3 / 8。。(注意这个结果不一定是整数。。。如果中间发生除 0 。。则该函数的结果为未定义,。。
。。。询问有多少 L 位的数。。其交错乘除的结果是 V 。。。
Analysis:
。。如果预处理处理消耗时间太多。。或者内存消耗太大。根本过不去。。。
。如果预处理太少。因为数据组数太多。。后面会 TLE 。。。
。所以这个题。。就是如何在预处理和事实计算中间。最大程度的利用题设中的限制条件。。。寻找平衡。。。。
。。以下是最重要的几点观察。。
- 询问的结果都是整数。
- 0 的情况非常特殊。。需要特判。
- 乘、除需要分开处理。。且都看做 “乘” 的情况。(把乘的结果记作 a,除的结果记作 b。。则就是找到计数所有满足 a / b = V 的 a 和 b 。。。
- 只需要考察 2, 3, 5, 7 四个因子。。
- 。5, 7 因子若出现。。都必然会完整的占据一个位子。。
。。综合考虑以上几点可得到算法。。
- 。枚举 a 或 b 其中一个的 5、7 因子。。则另一个的 5、7 因子可以计算出。。
- 。两次 DP 预处理。。第一次只考察乘积的情况。。_dp[i][p2][p3] 表示当前使用了 i 个位置。。产生了 p2 个 2 因子。和 p3 个 3 因子。的方案总数。。。
- 。第二次 dp[i][ii][p2][p3]。表示。乘数位置用了 i 个位置。。除数位置用了 ii 个位置。。产生了 p2 个 2 因子。。p3 个 3 因子。(这样就不需要考虑中间 p2 和 p3 指数为负数的情况。。。
- 。。通过组合数。计算最后结果。。。
。。。写的时候细节蛮多的。。。因为内存比较紧。。所有一直控制着数组大小。。
。数组开小了。卡了好久。。(但我一直都一边小心计算数组大小一边开的。。到现在还没明白是哪里开小了、、可见我真是弱爆了。。(。、嘛。。反正已经过了。。计算的那么仔细干嘛。。。。?。。
Level 2. Hotel Balifornia
Brief description:
。。阅读理解题。。
Analysis:
。。。很容易就注意到。中间的三阶线性递推序列是固定的。。大概是突破口。。
。。事实情况也就是如此。。开一个 set<pair<int, int, int>>。。来找循环节的位置。。
。。对于这个三阶线性递推序列。非常没有规律。。。所以打好表以后就把 set 去掉。。实际上只要打到最后一个可用位置出现的长度就可以、、
。。。。。观察发现这个值都不大。。剩下的模拟即可。。
(注意前后两个时间相等的情况。。
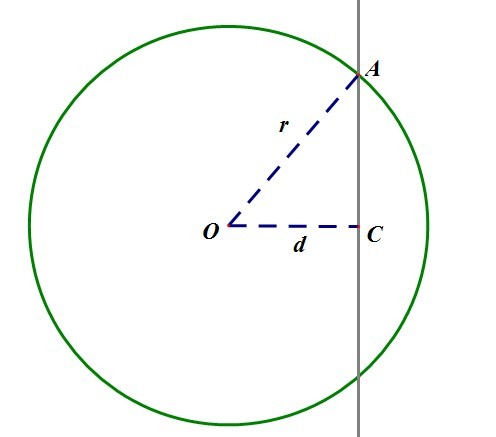
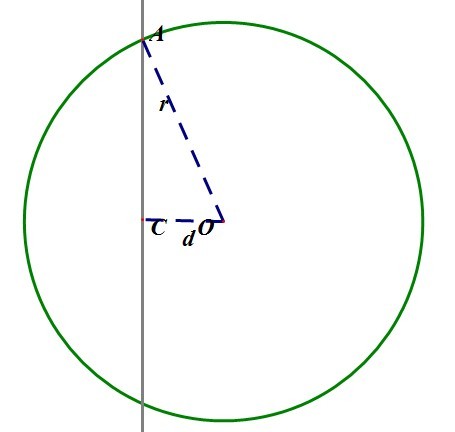
Level 2. A New Door
Brief description:
… 圆并周长。。(限制在一个矩形区域内。
Analysis:
… 这个就是比赛时把我坑出翔的那个题。。。。各种姿势提交了不下 20 页。。后来无耻的拉了所有我认识的系统学习过计算几何的神牛。。
(但是似乎没一个 AC 的。。。我都不好意思再坑其他人了。(哎呀捂脸。。、、、。。
。。。读了下解题报告。。发现所有能想到的可能坑的地方。。比赛时后来也都想到了。。。没办法只好拿标程出来。。拿我的代码一点点盖上去。直到把他搞 WA 。。。
。。。。基本算法就是陈鸿算法。。不会陈鸿算法的。。建议先学习陈鸿算法(Cheng’Hong’s Algorithm)。。
(。。比赛时有神牛 Java 1000 多 M 内存爆过去了。。我还以为是 Laguerre V 图。。非常高欣的以为赛后可以回收板子了。。结果其实打开一看还是陈鸿算法。。。。
。。考察圆与边界相交的情况。。右边界的情况基线 alpha 是 0 。。旋转角 beta 需要使用 acos 计算出来。。
。。。两个区间分别 alpha – beta 和 alpha + beta。。
。这里要分在矩形内部和外部两种情况讨论一下。。对于后者。。基线要取对称位置。。beta 要取负。。。
。。。。赛后发现其实也可以不讨论。。因为 acos 在负数的情况下可以返回钝角。。。
。。然后我改掉这个多余的讨论就 A 了。。。
。。。尼玛一口血就喷屏幕上了啊。。。我知道我是写丑了。。但是谁能告诉我这两个不是等价的吗。。。。
(代码发讨论版了。。求 debug 。。。
–UPD–
。。Bug 找到了。(。之前 Outcross() 函数在某种情况下会爆错、、、 /$:o~o
改正后的代码。。。带讨论。。..。不带讨论。。。
Level 3. Cucumber Boy and Cucumber Girl
Brief description:
。。给定 nn 个 n 阶方阵 A。。考察每对方阵乘积矩阵 D = Ai * Aj | 0 <= i < j < nn 。。 。。对于每个排列 P。。记 tr(P) 为所有 D[i][Pi] 中,是否有一项是奇数。。。 。。记 cnt(D) 为所有 tr 的和的奇偶性。。。求所有 cnt(D) 的和。。
Analysis:
… 很容易发现 cnt(D) 其实等价于其对应的积和式 % 2 的余数。。( perm(D) % 2。。
。。而 perm(D) == det(D) (mod 2)。。因此转换为相应矩阵的行列式。。
(。。方法是改变 D 矩阵每一项的奇偶性。。这样是存在奇数。。就变成了对应的积和式的乘积是否为 0 。。。
(。。而修改后的矩阵。。可以通过对 A 矩阵增加一列全是 1 的元素来得到。。
。。对于 perm(D) % 2 。这个是老套路了。。目前做到的大部分关于积和式的题目。。都归于了这种形式。。(。。求 perm(D) % 2^k 怎么做?。。
。。由此可以得到一个 O(nn^2 n^3) 的算法 。。
… 比赛的时候就一直卡在这一步了。。
。。读了一下题解。。发现后面需要用。。Cauchy–Binet formula
。。也就是将两个矩阵乘积的行列式。。分解为 n 个对应的余子式的乘积。。。
。。。由于我们只需要得到奇偶性。。整个求行列式的过程和分解以及组合的过程。。都可以通过位运算优化一维。。。
。。所以最后复杂度是 O(nn^2 + nn*n^2)。。
Level 4. A Fence for Byteland
Brief description:
… 给定两组点集。。求一个简单多边形。。划分开两组点集。。
。(允许点在多边形上。。这种情况下算相当于删除这个点。。。
Analysis:
… 第一反应是欧几里得 TSP 近似算法。。。后来因为圆并卡的太久。。就写了个多边形覆盖所有点的渣渣算法交上去了、、、太没追求了。!!。