Brief description:
。带边权版本的捉迷藏。。
Analysis:
先引用论文。。
路径剖分与树的分治的联系:
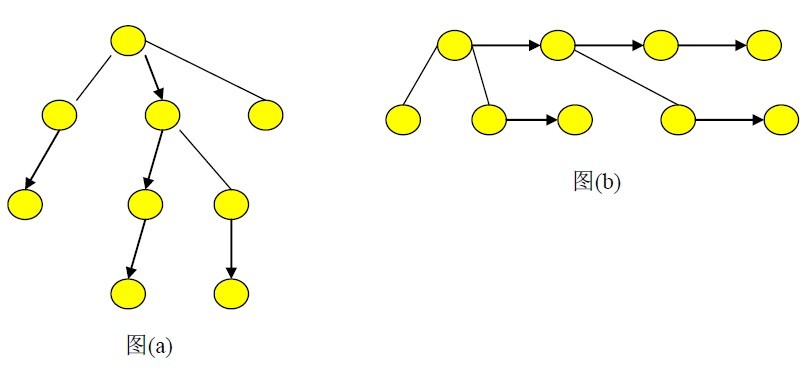
由于路径剖分与树的分治均可以解决树中路径的问题,我们不禁疑问,它们是否有着千丝万缕的联系呢?答案是肯定的。我们首先画出一棵树及其剖分 (如图(a)),我们似乎看不出有什么特殊,我们不妨把它的样子稍加改变 (如图(b)),按照点到根结点路径上的轻边个数分层摆放。
这时我们就能明显的看出路径剖分与树的分治两种算法其实有着惊人的相似,我们上一节中介绍了分治的两种方式:删除一个点,或一条边,而路径剖分相当于每次删除了一条链!所以路径剖分算法可以看做是基于链的分治,而且这种分治还有一个特点,每次被删除结点的儿子必将作为下一次删除的链的头结点。这样,就给我们的维护带来了方便。而正如我们第一节中讲的,每个点到根结点路径上的轻边个数是O(log N) 的,这样算法的时间复杂度便有了保证。
—————— 摘自 NOI 09 冬令营论文 《分治算法在树的路径问题中的应用》by qzc
上面这段话揭示了树链剖分的更深一层的含义,由此我们只要专注考察最高点经过一条重链这个子问题。
方法是线段树,左右各建立一组辅助信息,然后模仿 GSS 中的方法维护就可以了。
但是对于叶子的地方还要仔细处理,需要对每个结点建立一个大根堆,维护自此结点以下最远黑点距离。。
而维护这个堆。。又可以用更下层结点的线段树信息。。。(因为 “每次被删除结点的儿子必将作为下一次删除的链的头结点”。。
最后对所有的线段树,再建一个全局堆维护最终询问。。。
(。。总之这里的堆要涉及到复杂的修改操作,另外还需要支持询问次小值,必须手写。。。
修改的时候沿着跳链的方向,对堆和线段树交替维护即可。。复杂度 O(log^2n)。。。
树链剖分(4.7s +- 。。。
边分治(14.7s ++。。 。且存在一定几率会 T 。。反复提交可破。。。
(边分治的话不需要维护线段树,思考起来也更直接。。维护的时候直接记录每个点在哪些子树里,直接扫一遍过去就行了。。
(不过代码可变的地方也要多些,而且看起来的表现给人感觉不太稳定的样子。。。
(PS:.这样一来 QTREE 系列也就 ALL CLEAR 了。。。不过.。。好像这题现在已经成为路人题了吧?。。。