Brief description:
给定一个数组,你必须交换其中的两个数,最小化逆序对数。。
Analysis:
题目来源:http://www.ioi-jp.org/joi/2012/2013-ho/
问题 5:http://www.ioi-jp.org/joi/2012/2013-ho/2013-ho-t5-review.pdf
离线 + 线段树。
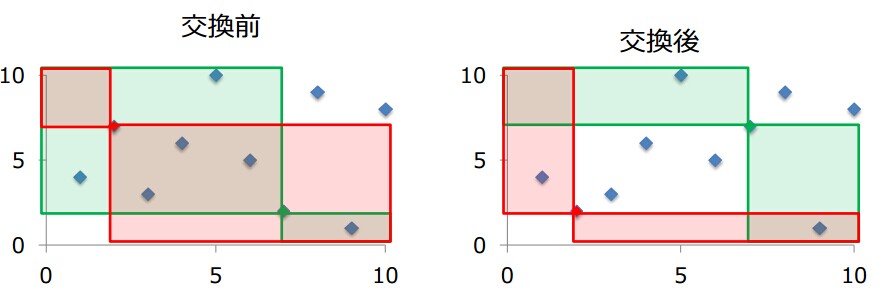
要点是数形结合。。一图流:
。。。交换两个数(前者比后者大)所获得的收益。。是 2*矩形中的面积)+ 1*边界的面积 + 1。。。(先不考虑边界)。。
问题现在便转化为检查这些极大子矩形。。。
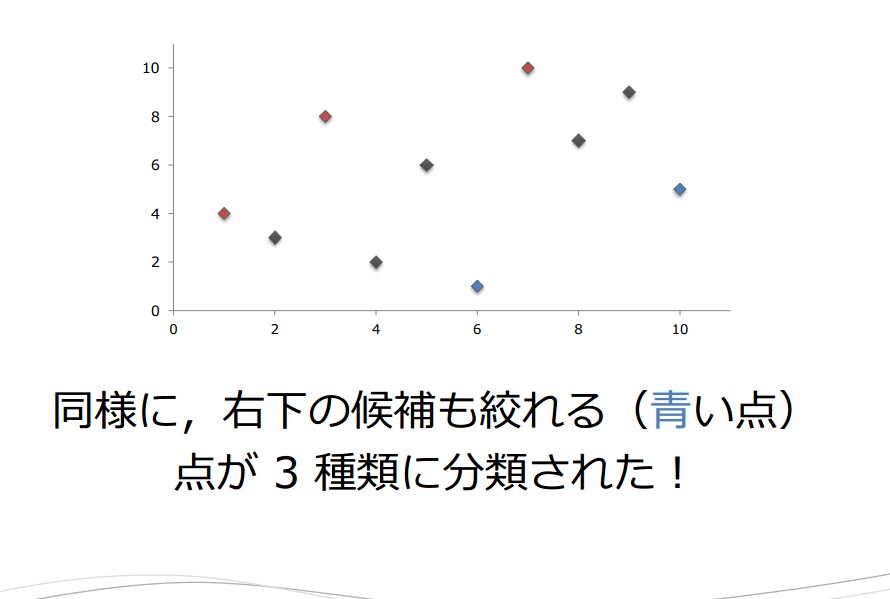
什么是极大子矩形呢?再来一张图:
极大子矩形一定是某个赤点和右下角的某个青点所组成的图形。。。
于是我们将点集(事件)分成三类。。赤点和蓝点都单调递增。。因此从左到右扫描线。、、记录每个事件离散化后的纵坐标。。
- 赤点(左上角):。。。在线段树中激活这个坐标。。
- 黑点(其他):。。加入这个事件。。将线段树中这个点坐标到最近激活赤点 += 2.。。
- 青点(右下角):。。。弹出所有纵坐标小于它的黑点(优先队列维护)。。区间求最值。。。
只需要区间加减,区间求最值。。线段树即可。。。
最后还要讨论各种边界的情况。。。
假设所有数都一样。。返回 0 。。。否则求出初始的逆序对 init_ans。。如果存在两个数相等。那么初始答案是 init_ans。。否则是 init_ans – 1。。
再讨论矩形的边界问题:
对于上边界:
。。当插入一个黑点时。。实际和这个黑点相等的那个坐标只能 += 1。。。
对于下边界:
。。当出现青点时。不仅要弹出所有小于它的黑点。。还要【消弱】等于它的黑点 -= 1。。。
//}/* .................................................................................................................................. */
const int N = int(1e5) + 9;
int a[N]; VI P; bool red[N], blue[N];
int n;
namespace ST{
#define lx (x<<1)
#define rx (lx|1)
#define ml (l+r>>1)
#define mr (ml+1)
#define lc lx, l, ml
#define rc rx, mr, r
#define rt 1, 1, P.size()
int T[4*N], D[4*N], a, b, d, ll, rr;
void upd(int x){
T[x] = max(T[lx], T[rx]);
}
void inc(int x, int d){
D[x] += d;
T[x] += d;
}
void rls(int x){
if (D[x]){
inc(lx, D[x]), inc(rx, D[x]);
D[x] = 0;
}
}
void add(int x, int l, int r){
if (b < l || r < a) return;
if (a <= l && r <= b){
inc(x, d);
}
else{
rls(x);
add(lc); add(rc);
upd(x);
}
}
void Add(int _a, int _b, int _d){
a = _a, b = _b, d = _d; add(rt);
}
int query(int x, int l, int r){
if (b < l || r < a) return 0;
if (a <= l && r <= b){
return T[x];
}
else{
rls(x);
return max(query(lc), query(rc));
}
}
int query(){
a = ll+1, b = rr; int z = a <= b ? query(rt) : 0; ++z;
return z;
}
}
namespace BIT{
int C[N], n;
int Sum(int x){
int z=0; for (;x;x^=low_bit(x)) z += C[x];
return z;
}
void Add(int x, int d){
for(;x<=n;x+=low_bit(x)) C[x] += d;
}
int Sum(int l, int r){
return Sum(r) - Sum(l-1);
}
} //using namespace BIT;
struct black{
int l, r;
black(int _l, int _r):l(_l),r(_r){
}
bool operator <(const black& rhs) const{
return l < rhs.l;
}
bool operator >(const black& rhs) const{
return l > rhs.l;
}
void add() const{
ST::Add(l, r, 2);
ST::Add(l, l, -1);
}
void del() const{
ST::Add(l, r, -2);
}
void weak() const{
ST::Add(l, r, -1);
}
};
priority_queue<black, vector<black>, greater<black> > Q;
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
#endif
REP_C(i, RD(n)) P.PB(RD(a[i])); UNQ(P);
BIT::n = P.size();
LL init_ans = 0; bool same = 0, all_same = 1; REP(i, n){
a[i] = LBD(P, a[i])+1;
init_ans += i - BIT::Sum(a[i]);
same |= (BIT::Sum(a[i]) - BIT::Sum(a[i]-1));
all_same &= (!i || a[i] == a[i-1]);
BIT::Add(a[i], 1);
}
if (all_same){
puts("0");
exit(0);
}
LL ans = init_ans + 1; if (same) --ans;
int t = 0; REP(i, n){
red[i] = checkMax(t, a[i]);
}
t = INF; DWN(i, n, 0){
blue[i] = checkMin(t, a[i]);
}
ST::ll = 0, ST::rr = -1;
REP(i, n){
if (red[i]){
ST::rr = a[i];
}
else if (blue[i]){
while (!Q.empty() && Q.top().l < a[i]){
Q.top().del();
Q.pop();
}
vector<black> QQ;
while (!Q.empty() && Q.top().l == a[i]){
Q.top().weak(); QQ.PB(Q.top()); Q.pop();
}
ST::ll = a[i];
checkMin(ans, init_ans - (ST::query()));
ECH(it, QQ) it->weak();
}
else{
black t = black(a[i], ST::rr);
Q.push(t); t.add();
}
}
OT(ans);
}




 Alca
Alca Amber
Amber Belleve Invis
Belleve Invis Chensiting123
Chensiting123 Edward_mj
Edward_mj Fotile96
Fotile96 Hlworld
Hlworld Kuangbin
Kuangbin Liyaos
Liyaos Lwins
Lwins LYPenny
LYPenny Mato 完整版
Mato 完整版 Mikeni2006
Mikeni2006 Mzry
Mzry Nagatsuki
Nagatsuki Neko13
Neko13 Oneplus
Oneplus Rukata
Rukata Seter
Seter Sevenkplus
Sevenkplus Sevenzero
Sevenzero Shirleycrow
Shirleycrow Vfleaking
Vfleaking wangzhpp
wangzhpp Watashi
Watashi WJMZBMR
WJMZBMR Wywcgs
Wywcgs XadillaX
XadillaX Yangzhe
Yangzhe 三途川玉子
三途川玉子 About.me
About.me Vijos
Vijos
