某岛

… : "…アッカリ～ン . .. . " .. .
October 20, 2011

ZOJ 3546. Advanture of Xiaoxingxing

Brief description:

翻纸盒问题，给定一个 N 个顶点的简单多边形，问沿着 x 轴进行滚动，触碰 T 点时翻滚的角度。
多边形的顶点按照顺时针或逆时针给出，且第一个点是源点，T 点一定在这个多边形的右边，所有点的 y 轴坐标 >= 0。
.. ( N <= 100 ).. .

Analysis:

。。。花了 5 个小时总算 A 掉了这个题。。可见现场赛的时候是根本写不出来的。。
么？。

。。这题的做法并不是很难想。。包括先求凸包、计算旋转用的外角、计算周长。。进行一次第一次翻滚（取模。。）。。
。。都是可以写的。。那么唯一的难点即使临近结束之时。。

。。。。例子。。

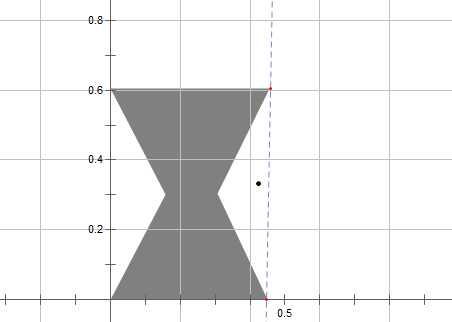
（如图所示，。。。目标点在“沙漏”形状的简单多边形的凹角里面。。
这种情况不会出现在初始的输入中，但是仍然可能出现在执行期。。）

。。那么看来后期不能一直用凸包进行操作。。原简单多边形还是要保存的。。
先给出主程序。。

.. .
int main() {

    //freopen("in.txt", "r", stdin);

	while (scanf("%d", &n) != EOF){

	    init(), cnt = int((T.x - C[cur].x) / perimeter) - 1;
        res = 2 * PI * cnt, T.x -= perimeter * cnt, cnt = 0;

		while (cnt < 2 * nn){
		    pivot = C[cur], alpha = cnt ? angle[cur] : (C[cur+1] - C[cur]).atan(); if (Roll()) break;
			T = rotate(T, alpha, pivot), res += alpha, ++cnt;
			if (++cur == nn) cur = 0;
		}

        if (cnt == 2 * nn) OT(no_solution);
        else OT(res);
	}
}
..

可以看到。。对周长取模之后。。至多再进行 2n 次 Roll() 操作。。
就一定会碰到那个交点（前提是有解。。之所以再进行 2n 次是因为无法很快的找到旋转过程中在最右边的点。。）
。。

（顺便一提。。根据运动的相对性。。 所有对多边形进行的操作。。都转化为对单个 T 点。。进行反向的操作。。）

唯一剩下的这个工作，就是简单多边形和一段弧线求交。。
。。枚举简单多边形的每一条边（。因为这一步的存在现在的复杂度是 O(n2) 的。。。有更好方法么？。。）

（ bool Roll() 函数。。 。。其中 alpha 表示这次旋转的最大角度。。beta 表示最小旋转多少度可以到达这个值。。
。。如果求完以后 beta 的值仍然不满足条件。。那么函数返回 false。。。。。。）

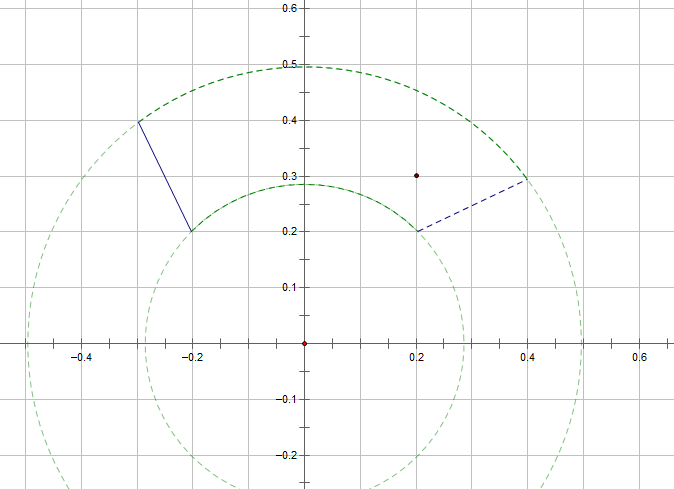
那么现在唯一剩下的工作就是。。线段和弧线求交。。
(。。我发现如果线段的延长线同圆心在一条直线上的话。。那么这个问题会非常好写。。。。)

。。。。对于这个一般的情况。。我们发现是一个定比分点的问题。。
。。。。。然后发现这里要解这个三角形。。
。。但是这么复杂的三角形问题。。我显然是不会解的。。。。

。。。。没办法了。。只好看看有没有别的方法。。。再多画几条线。。

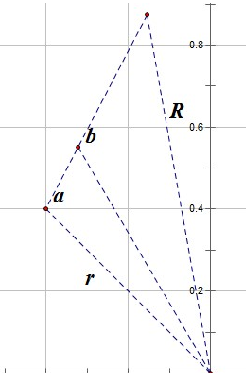
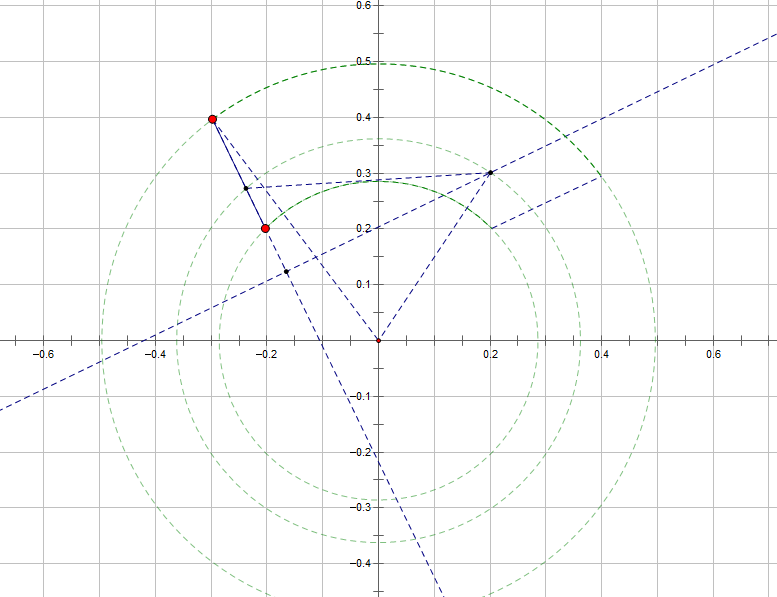
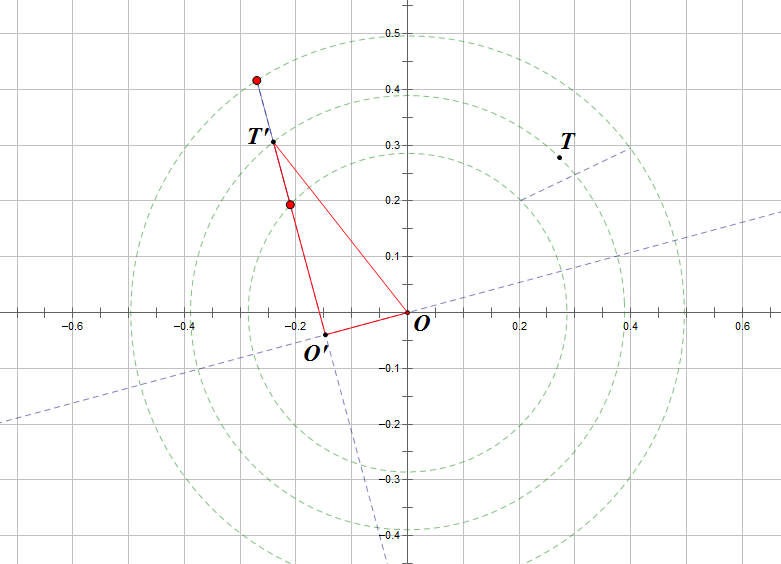
（。正确的方法是过源点 O（也就是旋转中心 pivot。。）做线段的垂足 O’。。
。。。。然后 O’ 到 T’ 的方向向量是可以通过图中的红三算出来的。。

这样就完成了。

。。（但是果然还是好复杂好复杂。。。。）。。

/** ` Micro Mezzo Macro Flation -- Overheated Economy ., **/

#include <algorithm>
#include <iostream>
#include <iomanip>
#include <sstream>
#include <cstring>
#include <cstdio>
#include <string>
#include <vector>
#include <bitset>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <list>
#include <set>
#include <map>

using namespace std;

#define REP(i, n) for (int i=0;i<int(n);++i)
#define FOR(i, a, b) for (int i=int(a);i<int(b);++i)
#define DWN(i, b, a) for (int i=int(b-1);i>=int(a);--i)
#define REP_1(i, n) for (int i=1;i<=int(n);++i)
#define FOR_1(i, a, b) for (int i=int(a);i<=int(b);++i)
#define DWN_1(i, b, a) for (int i=int(b);i>=int(a);--i)
#define REP_C(i, n) for (int n____=int(n),i=0;i<n____;++i)
#define FOR_C(i, a, b) for (int b____=int(b),i=a;i<b____;++i)
#define DWN_C(i, b, a) for (int a____=int(a),i=b-1;i>=a____;--i)
#define REP_N(i, n) for (i=0;i<int(n);++i)
#define FOR_N(i, a, b) for (i=int(a);i<int(b);++i)
#define DWN_N(i, b, a) for (i=int(b-1);i>=int(a);--i)
#define REP_1_C(i, n) for (int n____=int(n),i=1;i<=n____;++i)
#define FOR_1_C(i, a, b) for (int b____=int(b),i=a;i<=b____;++i)
#define DWN_1_C(i, b, a) for (int a____=int(a),i=b;i>=a____;--i)
#define REP_1_N(i, n) for (i=1;i<=int(n);++i)
#define FOR_1_N(i, a, b) for (i=int(a);i<=int(b);++i)
#define DWN_1_N(i, b, a) for (i=int(b);i>=int(a);--i)
#define REP_C_N(i, n) for (n____=int(n),i=0;i<n____;++i)
#define FOR_C_N(i, a, b) for (b____=int(b),i=a;i<b____;++i)
#define DWN_C_N(i, b, a) for (a____=int(a),i=b-1;i>=a____;--i)
#define REP_1_C_N(i, n) for (n____=int(n),i=1;i<=n____;++i)
#define FOR_1_C_N(i, a, b) for (b____=int(b),i=a;i<=b____;++i)
#define DWN_1_C_N(i, b, a) for (a____=int(a),i=b;i>=a____;--i)

#define DO(n) while(n--)
#define DO_C(n) int n____ = n; while(n____--)
#define TO(i, a, b) int s_=a<b?1:-1,b_=b+s_;for(int i=a;i!=b_;i+=s_)
#define TO_1(i, a, b) int s_=a<b?1:-1,b_=b;for(int i=a;i!=b_;i+=s_)
#define SQZ(i, j, a, b) for (int i=int(a),j=int(b)-1;i<j;++i,--j)
#define SQZ_1(i, j, a, b) for (int i=int(a),j=int(b);i<=j;++i,--j)
#define REP_2(i, j, n, m) REP(i, n) REP(j, m)
#define REP_2_1(i, j, n, m) REP_1(i, n) REP_1(j, m)

#define ALL(A) A.begin(), A.end()
#define LLA(A) A.rbegin(), A.rend()
#define CPY(A, B) memcpy(A, B, sizeof(A))
#define INS(A, P, B) A.insert(A.begin() + P, B)
#define ERS(A, P) A.erase(A.begin() + P)
#define BSC(A, X) find(ALL(A), X) // != A.end()
#define CTN(T, x) (T.find(x) != T.end())
#define SZ(A) int(A.size())
#define PB push_back
#define MP(A, B) make_pair(A, B)

#define Rush int T____; RD(T____); DO(T____)
#pragma comment(linker, "/STACK:36777216")
#pragma GCC optimize ("O2")
#define Ruby system("ruby main.rb")
#define Haskell system("runghc main.hs")
#define Pascal system("fpc main.pas")

typedef long long LL;
typedef double DB;
typedef unsigned UINT;
typedef unsigned long long ULL;

typedef vector<int> VI;
typedef vector<char> VC;
typedef vector<string> VS;
typedef vector<LL> VL;
typedef vector<DB> VD;
typedef set<int> SI;
typedef set<string> SS;
typedef set<LL> SL;
typedef set<DB> SD;
typedef map<int, int> MII;
typedef map<string, int> MSI;
typedef map<LL, int> MLI;
typedef map<DB, int> MDI;
typedef map<int, bool> MIB;
typedef map<string, bool> MSB;
typedef map<LL, bool> MLB;
typedef map<DB, bool> MDB;
typedef pair<int, int> PII;
typedef pair<int, bool> PIB;
typedef vector<PII> VII;
typedef vector<VI> VVI;
typedef vector<VII> VVII;
typedef set<PII> SII;
typedef map<PII, int> MPIII;
typedef map<PII, bool> MPIIB;


/** I/O Accelerator **/

/* ... :" We are I/O Accelerator ... Use us at your own risk ;) ... " .. */

template<class T> inline void RD(T &);
template<class T> inline void OT(const T &);

inline int RD(){ int x; RD(x); return x;}
template<class T> inline T& _RD(T &x){ RD(x); return x;}
inline void RC(char &c){scanf(" %c", &c);}
inline void RS(char *s){scanf("%s", s);}

template<class T0, class T1> inline void RD(T0 &x0, T1 &x1){RD(x0), RD(x1);}
template<class T0, class T1, class T2> inline void RD(T0 &x0, T1 &x1, T2 &x2){RD(x0), RD(x1), RD(x2);}
template<class T0, class T1, class T2, class T3> inline void RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3){RD(x0), RD(x1), RD(x2), RD(x3);}
template<class T0, class T1, class T2, class T3, class T4> inline void RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4), RD(x5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void RD(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5, T6 &x6){RD(x0), RD(x1), RD(x2), RD(x3), RD(x4), RD(x5), RD(x6);}
template<class T0, class T1> inline void OT(T0 &x0, T1 &x1){OT(x0), OT(x1);}
template<class T0, class T1, class T2> inline void OT(T0 &x0, T1 &x1, T2 &x2){OT(x0), OT(x1), OT(x2);}
template<class T0, class T1, class T2, class T3> inline void OT(T0 &x0, T1 &x1, T2 &x2, T3 &x3){OT(x0), OT(x1), OT(x2), OT(x3);}
template<class T0, class T1, class T2, class T3, class T4> inline void OT(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void OT(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4), OT(x5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void OT(T0 &x0, T1 &x1, T2 &x2, T3 &x3, T4 &x4, T5 &x5, T6 &x6){OT(x0), OT(x1), OT(x2), OT(x3), OT(x4), OT(x5), OT(x6);}

template<class T> inline void RST(T &A){memset(A, 0, sizeof(A));}
template<class T0, class T1> inline void RST(T0 &A0, T1 &A1){RST(A0), RST(A1);}
template<class T0, class T1, class T2> inline void RST(T0 &A0, T1 &A1, T2 &A2){RST(A0), RST(A1), RST(A2);}
template<class T0, class T1, class T2, class T3> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3){RST(A0), RST(A1), RST(A2), RST(A3);}
template<class T0, class T1, class T2, class T3, class T4> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4), RST(A5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void RST(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6){RST(A0), RST(A1), RST(A2), RST(A3), RST(A4), RST(A5), RST(A6);}

template<class T> inline void CLR(T &A){A.clear();}
template<class T0, class T1> inline void CLR(T0 &A0, T1 &A1){CLR(A0), CLR(A1);}
template<class T0, class T1, class T2> inline void CLR(T0 &A0, T1 &A1, T2 &A2){CLR(A0), CLR(A1), CLR(A2);}
template<class T0, class T1, class T2, class T3> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3){CLR(A0), CLR(A1), CLR(A2), CLR(A3);}
template<class T0, class T1, class T2, class T3, class T4> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4), CLR(A5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void CLR(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6){CLR(A0), CLR(A1), CLR(A2), CLR(A3), CLR(A4), CLR(A5), CLR(A6);}
template<class T> inline void CLR(T &A, int n){REP(i, n) CLR(A[i]);}
template<class T> inline void FLC(T &A, int x){memset(A, x, sizeof(A));}
template<class T0, class T1> inline void FLC(T0 &A0, T1 &A1, int x){FLC(A0, x), FLC(A1, x);}
template<class T0, class T1, class T2> inline void FLC(T0 &A0, T1 &A1, T2 &A2){FLC(A0), FLC(A1), FLC(A2);}
template<class T0, class T1, class T2, class T3> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3){FLC(A0), FLC(A1), FLC(A2), FLC(A3);}
template<class T0, class T1, class T2, class T3, class T4> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4){FLC(A0), FLC(A1), FLC(A2), FLC(A3), FLC(A4);}
template<class T0, class T1, class T2, class T3, class T4, class T5> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5){FLC(A0), FLC(A1), FLC(A2), FLC(A3), FLC(A4), FLC(A5);}
template<class T0, class T1, class T2, class T3, class T4, class T5, class T6> inline void FLC(T0 &A0, T1 &A1, T2 &A2, T3 &A3, T4 &A4, T5 &A5, T6 &A6){FLC(A0), FLC(A1), FLC(A2), FLC(A3), FLC(A4), FLC(A5), FLC(A6);}

template<class T> inline void SRT(T &A){sort(ALL(A));}
template<class T, class C> inline void SRT(T &A, C B){sort(ALL(A), B);}


/** Add - On **/

const int MOD = 1000000007;
const int INF = 0x7fffffff;
const DB EPS = 1e-6;
const DB OO = 1e15;
const DB PI = M_PI;

// <<= ` 0. Daily Use .,

template<class T> inline void checkMin(T &a,const T b){if (b<a) a=b;}
template<class T> inline void checkMax(T &a,const T b){if (b>a) a=b;}
template <class T, class C> inline void checkMin(T& a, const T b, C c){if (c(b,a)) a = b;}
template <class T, class C> inline void checkMax(T& a, const T b, C c){if (c(a,b)) a = b;}
template<class T> inline T min(T a, T b, T c){return min(min(a, b), c);}
template<class T> inline T max(T a, T b, T c){return max(max(a, b), c);}
template<class T> inline T min(T a, T b, T c, T d){return min(min(a, b), min(c, d));}
template<class T> inline T sqr(T a){return a*a;}
template<class T> inline T cub(T a){return a*a*a;}
int Ceil(int x, int y){return (x - 1) / y + 1;}

// <<= ` 1. Bitwise Operation .,

inline bool _1(int x, int i){return x & 1<<i;}
inline int _1(int i){return 1<<i;}
inline int _U(int i){return _1(i) - 1;};

inline int count_bits(int x){
    x = (x & 0x55555555) + ((x & 0xaaaaaaaa) >> 1);
    x = (x & 0x33333333) + ((x & 0xcccccccc) >> 2);
    x = (x & 0x0f0f0f0f) + ((x & 0xf0f0f0f0) >> 4);
    x = (x & 0x00ff00ff) + ((x & 0xff00ff00) >> 8);
    x = (x & 0x0000ffff) + ((x & 0xffff0000) >> 16);
    return x;
}

template<class T> inline T low_bit(T x) {
    return x & -x;
}

template<class T> inline T high_bit(T x) {
    T p = low_bit(x);
    while (p != x) x -= p, p = low_bit(x);
    return p;
}

// <<= ` 2. Modular Arithmetic Basic .,

inline void INC(int &a, int b){a += b; if (a >= MOD) a -= MOD;}
inline int sum(int a, int b){a += b; if (a >= MOD) a -= MOD; return a;}
inline void DEC(int &a, int b){a -= b; if (a < 0) a += MOD;}
inline int dff(int a, int b){a -= b; if (a < 0) a  += MOD; return a;}
inline void MUL(int &a, int b){a = int((LL)a * b % MOD);}
inline int pdt(int a, int b){return int((LL)a * b % MOD);}

// <<= '9. Comutational Geometry .,

struct Po; struct Line; struct Seg;

inline int sgn(DB x){return x < -EPS ? -1 : x > EPS;}
inline int sgn(DB x, DB y){return sgn(x - y);}

struct Po{
    DB x, y;
    Po(DB _x = 0, DB _y = 0):x(_x), y(_y){}

    friend istream& operator >>(istream& in, Po &p){return in >> p.x >> p.y;}
    friend ostream& operator <<(ostream& out, Po p){return out << "(" << p.x << ", " << p.y << ")";}

    friend bool operator ==(Po, Po);
    friend Po operator +(Po, Po);
    friend Po operator -(Po, Po);
    friend Po operator *(Po, DB);
    friend Po operator /(Po, DB);

    bool operator < (const Po &rhs) const{return sgn(x, rhs.x) < 0 || sgn(x, rhs.x) == 0 && sgn(y, rhs.y) < 0;}
    Po& operator +=(Po rhs){x += rhs.x, y += rhs.y;}
    Po& operator -=(Po rhs){x -= rhs.x, y -= rhs.y;}
    Po& operator *=(DB k){x *= k, y *= k;}
    Po& operator /=(DB k){x /= k, y /= k;}

    DB length_sqr(){return sqr(x) + sqr(y);}
    DB length(){return sqrt(length_sqr());}

    DB atan(){
        return atan2(y, x);
    }

    void input(){
        int _x, _y; scanf("%d %d", &_x, &_y);
        x = _x, y = _y;
    }
};

bool operator ==(Po a, Po b){return sgn(a.x - b.x) == 0 && sgn(a.y - b.y) == 0;}
Po operator +(Po a, Po b){return Po(a.x + b.x, a.y + b.y);}
Po operator -(Po a, Po b){return Po(a.x - b.x, a.y - b.y);}
Po operator *(Po a, DB k){return Po(a.x * k, a.y * k);}
Po operator /(Po a, DB k){return Po(a.x / k, a.y / k);}

struct Line{
    Po a, b;
    Line(Po _a = Po(), Po _b = Po()):a(_a), b(_b){}
    Line(DB x0, DB y0, DB x1, DB y1):a(Po(x0, y0)), b(Po(x1, y1)){}
    Line(Seg);
};

struct Seg{
    Po a, b;
    Seg(Po _a = Po(), Po _b = Po()):a(_a), b(_b){}
    Seg(DB x0, DB y0, DB x1, DB y1):a(Po(x0, y0)), b(Po(x1, y1)){}
    Seg(Line l);

    DB length(){return (b - a).length();}
};

Line::Line(Seg l):a(l.a), b(l.b){}
Seg::Seg(Line l):a(l.a), b(l.b){}


#define innerProduct dot
#define scalarProduct dot
#define dotProduct dot
#define outerProduct det
#define crossProduct det

inline DB dot(DB x1, DB y1, DB x2, DB y2){return x1 * x2 + y1 * y2;}
inline DB dot(Po a, Po b){return dot(a.x, b.y, b.x, b.y);}
inline DB dot(Po p0, Po p1, Po p2){return dot(p1 - p0, p2 - p0);}
inline DB dot(Line l1, Line l2){return dot(l1.b - l1.a, l2.b - l2.a);}
inline DB det(DB x1, DB y1, DB x2, DB y2){return x1 * y2 - x2 * y1;}
inline DB det(Po a, Po b){return det(a.x, a.y, b.x, b.y);}
inline DB det(Po p0, Po p1, Po p2){return det(p1 - p0, p2 - p0);}
inline DB det(Line l1, Line l2){return det(l1.b - l1.a, l2.b - l2.a);}

template<class T1, class T2> inline DB dist(T1 x, T2 y){return sqrt(dist_sqr(x, y));}

inline DB dist_sqr(Po a, Po b){return sqr(a.x - b.x) + sqr(a.y - b.y);}
inline DB dist_sqr(Po p, Line l){Po v0 = l.b - l.a, v1 = p - l.a; return sqr(fabs(det(v0, v1))) / v0.length_sqr();}
inline DB dist_sqr(Po p, Seg l){
    Po v0 = l.b - l.a, v1 = p - l.a, v2 = p - l.b;
    if (sgn(dot(v0, v1)) * sgn(dot(v0, v2)) <= 0) return dist_sqr(p, Line(l));
    else return min(v1.length_sqr(), v2.length_sqr());
}

inline DB dist_sqr(Line l, Po p){
    return dist_sqr(p, l);
}

inline DB dist_sqr(Line l1, Line l2){
    if (sgn(det(l1, l2)) != 0) return 0;
    return dist_sqr(l1.a, l2);
}
inline DB dist_sqr(Line l1, Seg l2){
    Po v0 = l1.b - l1.a, v1 = l2.a - l1.a, v2 = l2.b - l1.a; DB c1 = det(v0, v1), c2 = det(v0, v2);
    return sgn(c1) != sgn(c2) ? 0 : sqr(min(fabs(c1), fabs(c2))) / v0.length_sqr();
}

inline DB dist_sqr(Seg l, Po p){
    return dist_sqr(p, l);
}

inline DB dist_sqr(Seg l1, Line l2){
    return dist_sqr(l2, l1);
}

bool isIntersect(Seg l1, Seg l2){

    //if (l1.a == l2.a || l1.a == l2.b || l1.b == l2.a || l1.b == l2.b) return true;

    return
        min(l1.a.x, l1.b.x) <= max(l2.a.x, l2.b.x) &&
        min(l2.a.x, l2.b.x) <= max(l1.a.x, l1.b.x) &&
        min(l1.a.y, l1.b.y) <= max(l2.a.y, l2.b.y) &&
        min(l2.a.y, l2.b.y) <= max(l1.a.y, l1.b.y) &&
    sgn( det(l1.a, l2.a, l2.b) ) * sgn( det(l1.b, l2.a, l2.b) ) <= 0 &&
    sgn( det(l2.a, l1.a, l1.b) ) * sgn( det(l2.b, l1.a, l1.b) ) <= 0;

}

inline DB dist_sqr(Seg l1, Seg l2){
    if (isIntersect(l1, l2)) return 0;
    else return min(dist_sqr(l1.a, l2), dist_sqr(l1.b, l2), dist_sqr(l2.a, l1), dist_sqr(l2.b, l1));
}

inline bool isOnseg(const Po &p, const Seg &l){
	return sgn(det(p, l.a, l.b)) == 0 &&
        sgn(l.a.x, p.x) * sgn(l.b.x, p.x) <= 0 && sgn(l.a.y, p.y) * sgn(l.b.y, p.y) <= 0;
}

inline Po intersect(const Line &l1, const Line &l2){
    return l1.a + (l1.b - l1.a) * (det(l2.a, l1.a, l2.b) / det(l2, l1));
}

// perpendicular foot
inline Po intersect(const Po & p, const Line &l){
	return intersect(Line(p, p + Po(l.a.y - l.b.y, l.b.x - l.a.x)), l);
}

inline Po rotate(Po p, DB alpha, Po o = Po()){
    p.x -= o.x, p.y -= o.y;
    return Po(p.x * cos(alpha) - p.y * sin(alpha), p.y * cos(alpha) + p.x * sin(alpha)) + o;
}


// <<= ' 0. I/O Accelerator interface .,

template<class T> inline void RD(T &x){
    //cin >> x;
    //scanf("%d", &x);
    char c; for (c = getchar(); c < '0'; c = getchar()); x = c - '0'; for (c = getchar(); c >= '0'; c = getchar()) x = x * 10 + c - '0';
    //char c; c = getchar(); x = c - '0'; for (c = getchar(); c >= '0'; c = getchar()) x = x * 10 + c - '0';

}

const DB no_solution = -1;

int ____Case;
template<class T> inline void OT(const T &x){

    printf("Case %d: ", ++____Case);

    if (x == no_solution){
        puts("Impossible");
    }
    else {
        printf("%.2lf\n", x / PI * 180);
    }
}

/* .................................................................................................................................. */

const int N = 109;

Po P[N], P_[N], C[N], T; DB _, angle[N], perimeter;
int cur, cnt; Po pivot; DB alpha, res;
int n, nn;

#define p0 P_[0]
bool cpPolar(const Po &p1, const Po &p2){
    int t = sgn(crossProduct(p0, p1, p2));
    if (t == 0) return dist_sqr(p0, p1) < dist_sqr(p0, p2);
    return t == 1;
}

#define O pivot
bool Roll(){
    DB rr = (T - O).length_sqr(), o = (T - O).atan(), beta = OO, t;

	REP(i, n){
	    Line L = Line(P[i], P[i + 1]);
        Po O_ = intersect(O, L), D = (P[i+1] - O).length_sqr() > (P[i] - O).length_sqr() ? P[i+1] - P[i] : P[i] - P[i+1];
        D /= D.length(), D *= sqrt(rr - dist_sqr(O, O_));

        if (isOnseg(O_ + D, L)){
            O_ += D, t = (O_ - O).atan() - o;
            if (t < 0) t += PI * 2; checkMin(beta, t);
        }
	}

	if (sgn(beta, alpha) <= 0){res += beta; return true;}
	return false;
}

void init(){
    REP(i, n) P[i].input(); P[n] = P[0], T.input();
    CPY(P_, P), iter_swap(P_, min_element(P_, P_ + n)), sort(P_ + 1, P_ + n, cpPolar);

    nn = 0, C[++nn] = P_[0], C[++nn] = P_[1];

    FOR(i, 2, n){
        while (nn >= 2 && sgn(crossProduct(C[nn-1], C[nn], P_[i])) <= 0) --nn;
        C[++nn] = P_[i];
    }

    perimeter = 0, C[0] = C[nn]; REP(i, nn){
        if (C[i].y == 0) cur = i;
        angle[i] = (C[i+1] - C[i]).atan();
        perimeter += dist(C[i], C[i+1]);
    }

    angle[-1] = angle[nn-1];

    DWN(i, nn, 0){
        angle[i] -= angle[i-1];
        if (angle[i] < -PI) angle[i] += PI * 2;
        else if (angle[i] > PI) angle[i] -= PI * 2;
    }
}

int main() {

    //freopen("in.txt", "r", stdin);

	while (scanf("%d", &n) != EOF){

	    init(), cnt = int((T.x - C[cur].x) / perimeter) - 1;
        res = 2 * PI * cnt, T.x -= perimeter * cnt, cnt = 0;

		while (cnt < 2 * nn){
		    pivot = C[cur], alpha = cnt ? angle[cur] : (C[cur+1] - C[cur]).atan(); if (Roll()) break;
			T = rotate(T, alpha, pivot), res += alpha, ++cnt;
			if (++cur == nn) cur = 0;
		}

        if (cnt == 2 * nn) OT(no_solution);
        else OT(res);
	}
}

External link:

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3546

Further discussion:

。。。翻滚部分的时间复杂度是可以降低到 O(n) 的。。方法是从支点开始。。沿逆时针寻找第一次变号的位置。 (… sgn(dist(P[i], O) – dist(T, O)).. ) ..
这个部分可以用单调队列维护。。。为此我们需要保存凸包点到原点的映射。。
另外。。用解三角形的方法也是可以组多边形与弧求交的部分的。。但是我现在 WA 了。。
。。。。。。。。。。。

Posted by xiaodao
Category: ZOJ
Tags:

2 Comments to “ZOJ 3546. Advanture of Xiaoxingxing”

  1. a
    August 22, 2013

    那个图是用什么软件画的？
  2. xiaodao
    August 24, 2013

    几何画板。。。 /$:<

Leave a Comment



« | »

  • Archives

    open all | close all