题意
给定一张由 n 组有标号完全图形成的图,第 i 个完全图的结点数为 ai。这些完全图之间形成一个环,每个完全图中编号最大的点向下一个完全图编号最小的点连一条边。
问该图中生成森林的方案数。
分析
首先自然考虑完全图内部的情况,定义 ![]() 表示 n 点的完全图的生成森林方案数,
表示 n 点的完全图的生成森林方案数,
类似处理连通图时的方法,我们枚举 i 表示 0 号点所在的连通块中还有其它多少个点,可得转移方程:
(1) 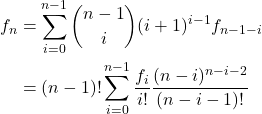
这里 ![]() 是经典的完全图生成树公式。上式进一步展开后可以发现卷积形式,可用分治 NTT 求解。
是经典的完全图生成树公式。上式进一步展开后可以发现卷积形式,可用分治 NTT 求解。
再考虑完全图之间的情况,考虑容斥。显然不合法的情况,只有环上边全部存在,且所有完全图中首尾均连通。
设这种情况是 ![]() ,只要把首位连起来考虑即可,转移和上面几乎一样:
,只要把首位连起来考虑即可,转移和上面几乎一样:
(2) 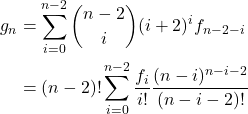
不用分治直接 NTT 就行了





