有一个东西叫做 labeled counting lemma。其实就是交代了 EGF 卷积的组合意义。
说的是给两个 EGF,F(x), G(x),那么 F(x)*G(x) 就是这两个对象重新标号之后所生成的对象的有序对,比如如果 C(x) 是连通图。那么 C^k(x)/k! 就是有 k 个连通分量的图,进一步就能推出 EGF 里 exp 的组合意义。
这个题多项式很容易构建,因为任意图都可以构建出 block-cut tree~
方法是我们思考有根版本的 C(x),那么这个根节点一定在一个 block 里,我们枚举这个 block 的 size i,那么这个 block 剩下的部分都能连一个 C(x)。。这部分就是 C(x)^(i-1),然后再乘以 b_i 就好。。。这个部分可以用 exp 表达。
剩下的是这个题的难点,就是拉格朗日定理。。其实有标号树就应该要学会这个。。只是那个问题里我们有太多方法可以逃课。。
在有根树问题里,移除了根节点之后,剩下的就是有根树本身的生成集族,所以有递归公式:
(1) ![]()
剩下的全都是拉格朗日反演的代数技巧,我们类比这种做法来解决点双和边双的计数问题,核心都是建立各自的 EGF 与 有根连通图 EGF 之间的关系,我们不妨也设它们分别为 b = B(x)、y = Y(x)。
点双和边双最大不同之处在于,一个割点可能同时存在于多个点双连通分量里。
考察点双,我们删除根节点 x 后,所剩下的部分是一些少了根节点的连通分量 t,那么 y 就是 e^t,所以我们只需考察 t 的 EGF。
我们可以枚举 t 中被删除的根节点 x 后所在的双连通分量的大小 i,那么这个连通分量中,除了 x 之外的其它节点都对应着一个独立的 y,于是有:
(2) 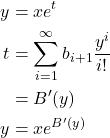
再考察边双,我们同样枚举根节点所在双连通分量的大小,那么删除这个双连通分量后,剩下的连通分量的每一个都会通过桥挂载到这个双连通分量中的任意节点,设这个部分是 t。
(3) 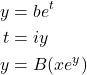
#include <lastweapon/poly>
using namespace lastweapon;
Poly H, HH;
int n;
LL C2(LL n) {
return n*(n-1)/2;
}
int b(int n) {
--n; if (!n) return 1;
Poly A(n); REP(i, n) A[i] = H[i] * -n;
Poly B = HH.mod(n) * A.exp();
return (B[n-1] * fac[n-1]).x;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
vector<int> q; DO(5) q.PB(RD()); n = *max_element(ALL(q)) + 1;
Poly C(n), G(n); REP(i, n) G[i] = Mint(2).pow(C2(i)), G[i] *= invFac[i]; C = G.log();
H = C.D().log(); HH = H.D();
for (auto i: q) printf("%d\n", b(i));
}





